Summary of the impact

The glass industry uses theoretical modelling to control, improve, and reduce the cost of designing and manufacturing novel glass products. Market-leaders [text removed for publication], Schott AG and Pilkington have developed modelling software which is underpinned by equations stemming from research at the University of Oxford.

[text removed for publication]. The same modelling approach is used in software developed by Schott which is now used in all of its modelling of drawing processes to reduce both development costs and the incidence of faults. Pilkington have implemented research performed at the University of Oxford to decrease the risk associated with manufacturing processes.

Underpinning research

Peter Howell has been working on extensional thin layer flows with application to the glass industry for the last 20 years. He first studied the evolution of thin sheets and jets of viscous fluid by taking a mathematical limit where the aspect ratio (the ratio of the thickness to the length or width) is small, precisely the situation in the manufacture of glass windows, tubing and optical fibres, for example. The result of the research [1] is a systematic framework for reducing the full Navier-Stokes equations to a simplified lower-dimensional system, which gives greater insight into possible instabilities and allows for much more efficient computation. These simplified models allow glass processes to be more effectively controlled to produce flawless products with optimised properties and to avoid catastrophic process failures.

In a glass furnace, many tiny gas bubbles are produced as the raw material melts and reacts. It is essential that all of these bubbles are eliminated before the glass leaves the furnace for further processing, to avoid defects in the finished product. To this end, the drainage of a bubble at the surface of a viscous fluid was modelled mathematically by Howell [2]; explicit formulae were found for the suction of fluid out of the thin film between the bubble and the atmosphere and for the expected timescale for a bubble to burst. Marangoni effects were incorporated in [3]; this allowed the influence of impurities on bubble bursting to be quantified. These analyses allow the required furnace residence time required to remove all bubbles, to be determined. Further research [4] allowed the deformation of any bubbles that do make it into the processing stage to be quantified.

Another important facet of the University of Oxford's glass modelling concerns the drawing of non-axisymmetric glass tubing. A key question is: what die shape is needed to make tubes of a given cross-sectional shape? Using ideas from perturbation theory and partial differential equations, researchers at the University of Oxford were able to solve this inverse problem explicitly [5, and other papers], as shown in the figure, which shows the die shape required to draw glass tubing with a square cross-section.

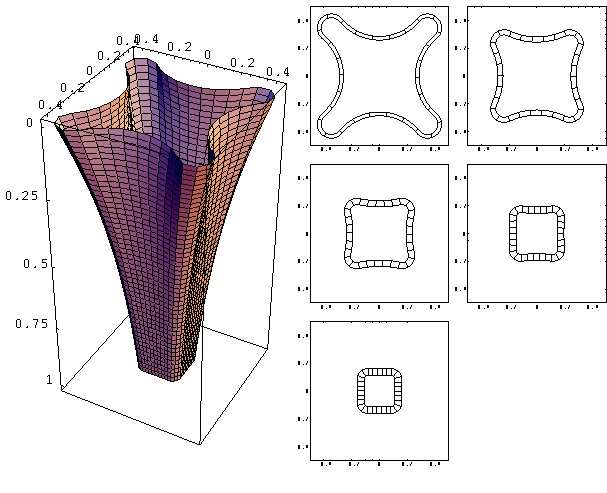
The gravitational sagging of heated glass sheets to form windscreens also provides an inverse problem, namely, to predict the temperature profile required to produce a final desired windscreen shape. In research carried out at the University of Oxford [6], this problem was analysed mathematically and found to reduce to an ill-posed partial differential equation which inevitably changes type from elliptic to hyperbolic across some interior line in the glass sheet.

The key researchers: Peter Howell (postdoc 1994-95, research fellow 1996-99 faculty 2001 to date); Chris Breward (postdoc 2001-03, research fellow 2003-08, faculty 2008 to date); Ian Griffiths (postdoc 2008-2010, Research fellow 2010 to date); Domingo Salazar (postdoc 1998-2002) were all at the University of Oxford when the research was carried out. At least four other researchers, including John Ockendon, participated in the University of Oxford's glass research programme.

References to the research

The three asterisked outputs best indicate the quality of the underpinning research. All six papers are in high quality internationally refereed journals. This is not an exhaustive list: results from many other papers have also led to impact on glass manufacturers.

Details of the impact

The University of Oxford's research on extensional thin layer flows has resulted in significant economic impact since 2008. The beneficiaries are the glass manufacturers [text removed for publication], Schott AG and Pilkington.

Pathways to impact:
[text removed for publication]

Between 2002 and 2006, the University of Oxford team (led by Prof. John Ockendon FRS) was a node in the €1.4m EU Research Training Network Math ematics for the Glass Industry: Computing and Analysis (known as MAGICAL) which aimed to promote collaborations between Universities and glass companies across the EU, including Schott AG. Schott AG posed specific research questions which were tackled by the MAGICAL team at the University of Oxford, and gained access to the University of Oxford's pre-existing research base relevant to glass flows.

Finally, Pilkington (now NSG group) has had a long standing relationship with the University of Oxford's Mathematical Insitute through Industrial Workshops organised by the Oxford Centre for Industrial and Applied Mathematics (OCIAM) and was also involved in MAGICAL. The current Head of the Float and Rolled Glass Technology Group says [B] "Pilkington Group research — in recent years the NSG European Technology Centre, have for many years found the OCIAM group to be much the most valuable point of contact for problems raising complex mathematical issues in glassmaking and glass products."

Nature and extent of the impact:

The glass industry constantly seeks improved models for production and processing technologies, so that it can reliably design and build improved, fault-free products while cutting development costs and innovating new advanced materials. It is understandable that major industrial glass producers, such as [text removed for publication] and Schott, were interested in the University of Oxford's research into modelling thin viscous sheets.

[text removed for publication]

At Schott AG, another world-leading glass and materials company with global sales of €2 billion (in 2011/12), research from the University of Oxford has been used even more widely. Like [text removed for publication], Schott has developed software, based on Howell's methodology for modelling thin viscous sheets and fibres, which is key in the improvement and development of glass forming processes. A senior scientist in the Mathematical Simulation and Optimization group states [D] "At Schott, we now have models based on these methods for all our drawing processes. A typical application is the prediction of suitable process conditions (heater power distribution, top roller speeds etc) for a desired glass sheet thickness and net width in the float process." Schott use the models to save significant sums in development costs. The senior scientist states [D] "In many cases, our only option in the development process are experiments in the actual production plant. A day in a typical production plant costs about 50,000 Euro. I am quite certain that the models saved us years of such experiments at the plants." In a subsequent email he confirms that these years of effort were post-2008.

One of Schott's major production processes, tube drawing, has also been heavily influenced by the University of Oxford's research into pressure-driven flows and hollow-fibre production. In particular, the asymptotic solutions developed at the University of Oxford have been used to create models which Schott claims offer improved accuracy over competing models. The senior scientist in the Mathematical Simulation and Optimization group states [D] "The results in [5, published in 2008, and other papers] are of special significance for the tube drawing process, one of Schott's major production processes. These asymptotic solutions for non-circular tube geometries are in my opinion superior to "brute force" numerical approaches which suffer from inaccuracies arising from the high glass viscosities downstream." This allows manufacturing processes for proposed new products to be reliably tested and optimised computationally, leading to significant savings in wastage and money.

Finally, work from the University of Oxford has allowed Schott to produce glass with fewer faults. Research into levitating thin sheets of glass on air cushions has allowed Schott to reduce dramatically the occurrence of instabilities in numerous moulding processes, and understanding of the presence of defects such as bubbles has helped them reduce the incidence of faults in many different glass-forming processes.

Pilkington is one of the leading glass suppliers in the UK and is now part of the Japan-based NSG Group which has manufacturing operations in 29 countries and global sales of over £4 billion. The company uses research carried out at the University of Oxford in several areas concerned with risk management, which is an essential part of production processes. The support the University of Oxford has provided with solving the problem of bubbles bursting on the surface of glass has given Pilkington invaluable understanding of the underlying physical processes (subsequently verified experimentally) as well as significant financial savings by avoiding lost production costs. The Head of the Float and Rolled Glass Technology Group at NSG states [B] "The idea that distinctions which could be drawn between various types of bubble develops a way of analysing melting problems which results in a better chance of taking the most appropriate action".

A common procedure in the manufacture of windscreens involves heating a sheet of glass so that it sags under gravity into the desired shape. The inverse problem of determining the heating profile required to produce a particular shape after sagging is tackled in the industry using computational modelling, which is found to be extremely delicate. The University of Oxford's mathematical research on this problem has been very useful for Pilkington, who found that "guidance as to how much can safely be left to automated algorithms and what requires active intervention by the user is hugely valuable in reducing product development time" [B].

Sources to corroborate the impact

[A] [text removed for publication]

[B] Letter from Group Head, Float and Rolled Glass Technology Group, NSG, describing the influence of Oxford's research on their product development. Copy held by the University of Oxford.

[C] [text removed for publication]

[D] Letter and emails from a Senior Scientist in the Mathematical Simulation and Optimisation Group, Schott AG, describing the impact of 10 relevant Oxford Mathematics publications on Schott's activities. Copies held by the University of Oxford.